Se denomina interferencia de la luz al hecho de que al superponerse dos o más ondas luminosas en un punto, bajo ciertas condiciones, la iluminación en ese punto no es igual a la suma de las iluminaciones que tendría si cada una de ellas llegara en ausencia de la otra o las restantes
No importa que las ondas sean transversales o longitudinales, o que tengan naturaleza mecánica o electromagnética.
Se utilizan valores medios pues todo detector de luz, sea el ojo humano, un instrumento de medición fotosensible, etc. posee cierta inercialidad; es decir, no registra valores instantáneos de la intensidad de las ondas luminosas, sino valores medios en intervalos de tiempo grandes en comparación con los tiempos de emisión de los átomos.
Cuando se produce la interferencia, en esa región la iluminación no es uniforme, aparece una sucesión de zonas claras y oscuras llamadas patrón de interferencia o cuadro interferencial.
Las ondas luminosas, sus oscilaciones, las fuentes o sus oscilaciones, los haces de luz en general son llamados coherentes.
Por tanto la interferencia consiste en la superposición de ondas coherentes o, por el contrario, las ondas coherentes son las que dan lugar a la interferencia.
Consideremos un medio óptimamente homogéneo en el que existen dos fuentes puntuales de ondas sinusoidales, esféricas, próximas entre si (F1 y F2) y con la misma frecuencia angular w. SeanE1 y E2 las perturbaciones ópticas que arriban desde las dos fuentes a un punto P, que por simplicidad consideremos alejado de las mismas.
Las magnitudes de las perturbaciones están dadas por:
Donde S1 y S2 son las distancias al punto P, Ф1 y Ф2 son las fases iniciales de las perturbaciones en F1 y F2, además K = (2 п)/ג es el número de onda. Los factores A1 y A2 representan las amplitudes de las perturbaciones y dependen de la potencia de las fuentes y de las distancias S1 y S2 respectivamente.
La perturbación resultante en el punto P será:
que puede escribirse en la forma :
, siendo: 
, siendo: 
La intensidad instantánea de la perturbación resultante en P es proporcional a E2 Por otro lado, la intensidad medida por los instrumentos es proporcional a E2 promediado en el tiempo. Considerando las expresiones anteriores puede demostrarse que:
De las expresiones 5 y 7 se comprende que la intensidad luminosa resultante depende de la diferencia
y por tanto del punto donde se mida. Esto significa que la energía luminosa no se distribuye monótona mente en la región de superposición sino que, como se muestra en la figura 2, se forma el patrón de interferencia o cuadro interferencial, caracterizado por la sucesión de zonas claras y oscuras. 
Geometría en el experimento de Young.
Para obtener la expresión de trabajo, consideremos el esquema que se muestra en la figura 3.Una rendija F deja pasar un estrecho haz de luz proveniente de la fuente luminosa L. Por difracción en F la luz llega a las rendijas F1 y F2 y los rayos que de aquí emergen interfieren en P sobre la pantalla.
La diferencia de recorrido óptico coincide con la diferencia de camino geométrico si n=1 (vacío).
lo cual se indica en el gráfico. Al plantear (8) consideramos que D es mucho mayor que d, de manera que los rayos r1 y r2 puedan considerarse paralelos entre sí con buena aproximación.
La diferencia de fase será entonces:
Si en P se tiene un máximo de intensidad, se cumple que:
La expresión (10) refleja la simetría del patrón respecto al máximo central ( m=0 ), situado en el centro C de la pantalla.
Del gráfico puede tenerse la relación:
, entonces 
y nos queda: 
para la franja brillante contigua ( m+1 ) se tendrá que:
La distancia lineal sobre la pantalla
entre los dos máximos de orden m y m+1 será entonces: 
y la separación angular
para los mismos, respecto al punto o será:
Es importante observar que bajo las consideraciones hechas, la distancia entre dos franjas brillantes consecutivas no depende de m.
La expresión (14) es la que utilizaremos en esta práctica y la (15) se aplica frecuentemente en las clases prácticas.
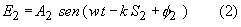
No hay comentarios:
Publicar un comentario